Kalyan Shrestha, Ph.D.
Computational Physicist, CFD Scientist
2kalyanshrestha@gmail.com |
About
I am a computational fluid dynamicist and multiphysics engineer with extensive industrial and academic experience in fluid mechanics, heat transfer, and multi-physics simulations. I have utilized, customized, and developed a wide range of CFD tools, including commercial solvers (STAR-CCM+) and in-house codes (Lattice Boltzmann framework, JHU LES code, MIT general circulation model), to address complex problems across aerospace, advanced manufacturing and geophysical fluid dynamics. Currently (2022 - present), I am a Research Engineer at Global Engineering and Materials, Inc., Princeton, New Jersey.
​
In my current R&D work, I lead the development of high-fidelity digital twin tools for complex multi-physics and multi-scale industrial process simulations and thermal-fluid systems. My work spans a wide range of coupled phenomena, including multiphase flows (VOF), flow through porous media, conjugate heat transfer (CHT), LES/RANS turbulence, rigid body motion, rapid cooling of metals, electromagnetic heating of composites, and fluid–structure interaction (FSI) within realistic industrial process environments. I am involved across the entire modeling and simulation lifecycle -from in-depth literature review and physics-based model development to adaptive meshing strategy design, simulation planning, and test strategy definition. My responsibilities further include CAD-to-CFD automation, workflow customization, large-scale parametric studies, root-cause investigations, data analytics, experimental validation, and process optimization. The overarching objective is to deliver actionable, physics-based insights that balance throughput and part quality while reducing production time and cost. These efforts have directly enabled the development of high-fidelity, computationally efficient, and robust digital twin solutions for challenging industrial thermal-fluid applications.
​
My past academic experiences cover a broad spectrum of research fields related to mechanical engineering and physical oceanography. My work explored the physics of boundary layer turbulent processes in the ice-free/ice-aware upper ocean and atmospheric surface layer and in developing parameterization schemes for climate models to improve the predictability of Earth’s environment. Earth's geophysical fluid dynamical processes have length scales and time scales that span over several orders of magnitude, and all of these processes in all scales can interact with each other, making this a challenging system to solve. At the University of Washington-Seattle, my work was focused on understanding the interactions between sea ice and submesoscale ocean variability. I used ocean-ice models to design idealized high-resolution numerical experiments to explore the underlying physics and devise parameterizations relevant to improving the predictive capabilities of the models of the rapidly changing polar regions. At UT Dallas, my research focussed on understanding the kinematic characteristics of Langmuir turbulence in coastal zones and developing theoretical models to assess the coherence and strength of coastal Langmuir Circulations. My research efforts at Lille 1 University, France contributed to the development of three-dimensional Lattice Boltzmann code to study convective, turbulent flows.​
​
​
​
​
Industrial R&D Work
Below is a summary of key digital twin solutions developed to address real-world engineering challenges.
1. SMARTCLAVE - Digital Twin for Autoclave Curing of Composites
Led the development of SMARTCLAVE, a high-fidelity digital twin incorporating integrated multi-scale, multi-physics sub-models to predict process-induced material responses, including defects and distortion, during autoclave curing of fiber-reinforced composite aerospace components. A distinguishing capability of SMARTCLAVE is its advanced thermal CFD module, which generates spatially and temporally varying, physics-based heat transfer coefficient (HTC) maps arising from the interaction between turbulent flow and convective heat transfer. These HTC maps drive tightly coupled thermochemical, consolidation, and stress models for downstream finite element analysis. SMARTCLAVE accurately captures the 3D evolution of temperature, resin pressure, and degree of cure, while predicting local defects such as voids, delamination, resin-rich regions, and ply waviness, as well as mesoscale part distortion. The tool has been deployed with a user-friendly GUI, enabling practical adoption in industrial environments.
2. QLAB - Digital Twin for Quenching of Metallic Workpieces
Led the development of QLAB, a high-fidelity digital twin for the quenching of metallic workpieces, enabling rapid tailoring of process conditions to minimize distortion in aerospace forging components. QLAB captures the multi-phase, multi-physics nature of quenching, including distinct heat transfer regimes, vapor blanket formation, boiling and convection heat transfer, agitation systems within realistic quench tank environments, air-to-water immersion dynamics, microstructural evolution, and thermomechanical response. The framework consists of a thermal CFD model sequentially coupled with an MTS-Precipitation microstructure model. The CFD model resolves turbulent flow, multiphase transformations, and complex quenching heat transfer stages (vapor blanket, nucleate boiling, and convection) to predict transient temperature fields. These thermal histories drive the MTS-Precipitation model, which captures microstructural precipitate evolution and its impact on material behavior. A user-friendly GUI was also developed for QLAB to support rapid industrial deployment.
This work was recognized with Best Paper Awards at the 2024 and 2025 Vertical Flight Society Forum international conferences.
3. Digital Twin for Microwave Curing of Thermoset Composites
Developed a novel multi-physics modeling framework for simulating the microwave curing of thermoset composites, where electromagnetic energy (300 MHz-300 GHz) is delivered via magnetrons positioned along the cavity walls. The key innovation lies in solving Maxwell’s equations using a magnetic vector potential formulation, which reduces computational cost by approximately 50 times compared to conventional approaches, while maintaining high-fidelity electromagnetic field resolution. The model predicts electromagnetic field distribution within the microwave cavity and its interaction with anisotropic composite materials to compute volumetric heat generation and resulting temperature evolution.
The long-term objective is to deliver a closed-loop digital twin for rapid process tailoring and optimization of microwave parameters, enabling homogeneous temperature and cure profiles while reducing defects such as porosity, resin-rich regions, delamination, wrinkling, and warping. The combined cost, time, and energy advantages of microwave-based curing-when integrated with digital twin capabilities-present strong potential for next-generation composite manufacturing and large-scale component production.
4. Digital Twin Framework for Resin Transfer Molding
Contributed to the development of a flow–stress coupled digital twin framework for Resin Transfer Molding (RTM), aimed at mitigating infusion-induced trapped air voids and curing-induced distortion. RTM is a key enabler for manufacturing integrated aerospace structures, reducing reliance on thousands of fasteners and mitigating corrosion-related sustainment costs. The developed framework integrates an infusion flow model based on Darcy’s law with a curing-induced stress model, leveraging a temperature- and cure-dependent multi-scale FEA formulation. This unified framework predicts pressure fields, flow-front evolution, residual stress, and deformation, enabling simulation-guided process optimization and reducing costly trial-and-error iterations. The model’s effectiveness was demonstrated through an industry use case with Spirit AeroSystems involving a representative composite fuselage structure.
5. Digital Twin for Additive Friction Stir Deposition
Contributed to the development of a PSPP (Process-Structure-Property-Performance) digital twin for large-scale Additive Friction Stir Deposition (AFSD), supporting optimization of process parameters for high-quality aerospace structural components with complex geometries. AFSD is a promising solid-state additive manufacturing technology that combines friction stir principles with layer-by-layer deposition, enabling near-net-shape fabrication with superior mechanical properties. The digital twin integrates a thermal CFD model capturing heat generation, plastic flow, material mixing, and tool-workpiece interaction; a microstructure evolution and precipitation model; a digital constitutive model based on crystal plasticity; a crack propagation model; and a total life prediction module. My contributions focused on enhancing the thermal CFD module for layer-by-layer deposition using VOF-based interface tracking, viscoelastic formulations for plasticized metal flow and mixing, and stick-slip contact models for tool-workpiece interaction. Computational efficiency was achieved through adaptive mesh refinement and moving mesh strategies to account for tool rotation and translation.
Academic Research
1. Submesoscale-Induced Basal Melting of Ice Shelf Cavities in Polar Regions
Several ice shelves in the Arctic’s and Antarctica’s coastlines have dramatically collapsed in very recent times (e.g. Brunt Ice Shelf - February 26, 2021; Milne Ice Shelf -August 4, 2020; Pine Island Glacier - February 2020, etc.). Such events can result in global sea level rise (around 0.24 inches rise was recorded from just 2018 to 2019) and pose an increased threat to the world’s coastal population. For an accurate assessment of ocean-forced glacier mass loss, global ocean models need to incorporate all key processes that bring heat toward the ice shelf base and enhance melting. Coarse-resolution climate projection models may be under-representing one of the key influences from the ocean eddies of a few km in size. In this study, we provide an argument that the effect of those eddies is significant and needs to be accounted for more accurate predictions of ice shelf basal melting and future projections of global sea level rise.
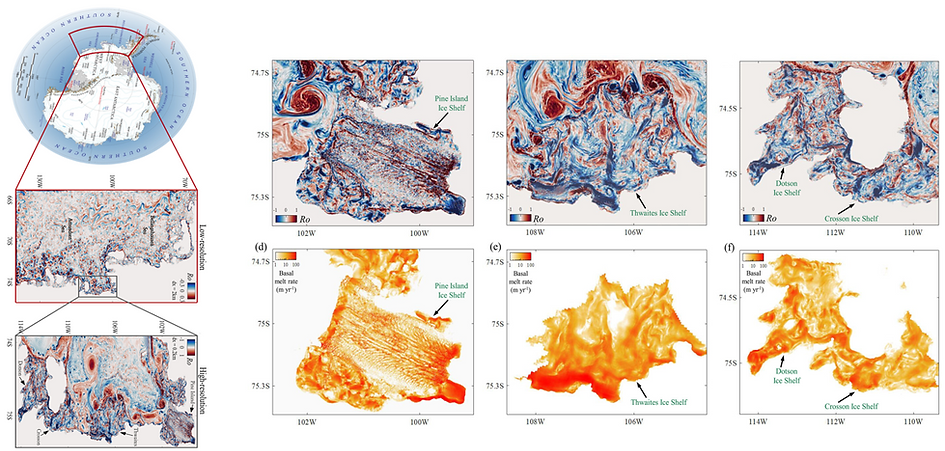
Ice shelf cavities in the Antarctica region highlighting highest basal melting near the grounding line
2. Physical Processes In The Upper Ocean
Earth's climate and ecosystem are mainly governed by three components: ocean, atmosphere, and sea ice, and the coupled interactions between them. Each of these components is comprised of a large number of physical, chemical, and biological processes with length scales and time scales varying over several orders of magnitude, and all these processes in all scales interact with each other. Thus, the Earth system is a non-linear, complex, gigantic problem to solve. One of the viable research techniques to address such a problem is the global climate model (GCM), where the Earth system processes are represented with mathematical equations and computationally solved using supercomputers. The equations are solved in a 3D grid of cells that cover the Earth's surface. Hence, it is easy to understand that the processes larger than the model grid size are fully resolved, and the subgrid-scale processes need to be parameterized.
Ocean surface mixed layer acts as a gateway between the atmosphere, sea ice, and ocean interior, mediating the exchange of heat, mass, momentum, and other tracers, and thus plays a crucial role in global climate. My research is focused on two of the most important surface mixed layer processes: (1) Ocean boundary layer phenomenon called Langmuir Circulations (2) Submesoscale mixed layer restratification. Since both of these processes are typically smaller than the GCM model resolution in terms of length scales, thus I am interested in exploring their underlying physics and developing/improving parameterization schemes for climate models.
​
​
​
a. Submesoscale Mixed Layer Restratification Under Sea Ice
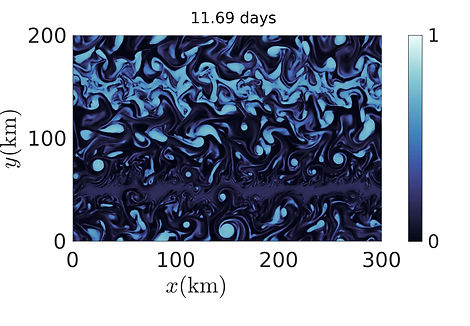
c = 0.2
Idealized simulation of frontal spindown in marginal ice zones
sea ice concentration
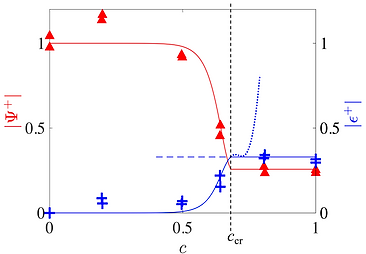
Overturning streamfunction vs. sea ice concentration
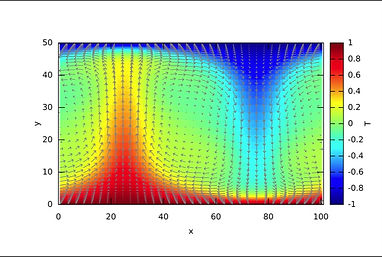
The ocean surface is filled with fronts that can become unstable to ageostrophic baroclinic instabilities and lead to the formation of submesoscale (SM) eddies in the ocean mixed layer (ML). These instabilities convert the lateral density gradients into vertical gradients and overturn the density fronts releasing potential energy. It is known that the vertical fluxes due to SM ML eddies play a significant role in the ML buoyancy budget. Also, the restratification process associated with the overturning of the fronts strongly influences variations in the ML depth. Hence, understanding the ML restratification process is of first-order importance in improving the accuracy of global climate models.
Fox-Kemper and Ferrari (JPO, 2008) showed that the MLE-induced restratification process could be cast in terms of an eddy-driven overturning streamfuntion such that eddy fluxes of density and other tracers can be approximated. Given its simple formulation and its accuracy in predicting changes to the buoyancy, it has been incorporated in many, if not all, climate projection models.
​
​
Parameterization of Fox-Kemper and Ferrari (JPO,2008)
:
where, are ML depth, lateral buoyancy gradients and the Coriolis parameter
is the vertical structure of overturning streamfunction
= 0.06-0.08
In our study, we found that the presence of sea ice cover induces a strong coupling between sea ice and surface ocean and hence strongly affects the ML restratification process. However, the conventional parameterization does not take into account the presence of sea ice in any way while being used in ice-covered polar oceans. Thus, we developed an improvement to the existing ML overturning parameterization, making it explicitly dependent on sea ice concentration,
​
​
Our parameterization scheme under sea ice
:
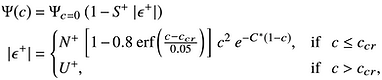
where,
The updated parameterization scheme predicts the reduction of the overturning streamfunction up to a factor of 4 for fully ice-covered regions with the sharp transition of submesoscale eddy characteristics occurring at critical sea ice concentration. The inclusion of such parameterization in global climate models can improve the representation of ocean-ice interactions and consequently lead to more accurate sea ice predictions.
b. Coastal-zone Langmuir Turbulence
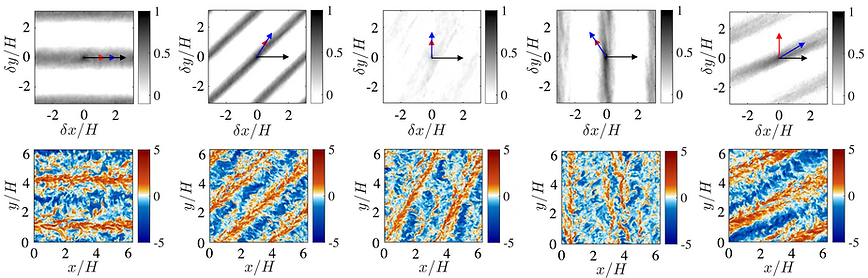
Effect of oblique wind (blue arrow), wave (red) and mean current (black) forcing on LC orientation
The ocean boundary layer (OBL) occupies the upper ≈100 m of Earth’s oceans and is forced by atmosphere-ocean and sea ice-ocean momentum fluxes, wave dynamics, and buoyancy. Foremost among OBL flow states is Langmuir turbulence – formed in response to simultaneously present wind and wave loading – resulting in the formation of streamwise-elongated, counterrotating Langmuir cells (LC). LC is a key contributor to vertical mixing and transport of materials in the upper mixed layer of the ocean and significantly contributes to physical and geochemical processes relevant to oil spill turbulent dispersion, ecology in the upper ocean, and parameterization of climate models. LC in coastal regions is an even more complex phenomenon further influenced by bottom-boundary layer shearing. Coastal-zone Langmuir turbulence is of pivotal importance to sediment erosion and resuspension, turbidity, dispersion of anthropogenic quantities, coastal biodiversity, etc. however, only a minority of preceding studies have addressed its characteristics.
Our study on the characteristics of LC in coastal regions have led to some interesting findings that have been summarized below:
(1) We presented evidence that intense downwelling and upwelling within the coastal LC induce phase-locked modulation of bathymetric stress.
(2) We explored the distinctive structural attributes of coastal LC compared to open-ocean LC and the ''cause and effect'' dynamics of wind and wave forcing (wind stress, wavenumber of the surface waves, and Stokes drift surface velocity) with their spatial length scales.
(3) We showed that oblique forcing between mean current associated with tidal currents, surface wave field, and atmospheric wind current in coastal zones influence the orientation of resultant coastal LC and provided theoretical justifications for the numerical results. Also, a model to predict the orientation was proposed.
Prognostic model to predict resultant LC orientation angle:
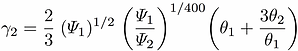
where,
= ratio of wind shear velocity to the bottom-wall friction velocity
= ratio of surface Stokes drift velocity to the bottom-wall friction velocity
= angle between wind stress and mean current forcing direction
= angle between Stokes drift vector and wind forcing direction
3. Lattice Boltzmann Method for Turbulent Flows
Simulation of Rayleigh-Benard convection using FV LB method
Lattice Boltzmann Method (LBM) has emerged as a viable alternative to Navier-Stokes Direct Numerical Simulations (NS DNS) in fluid dynamics research. It is based on the mesoscopic level of the description that goes beyond the Navier-Stokes continuum matter description of fluids and can handle complex effects, such as the interaction between different fluid components, phase-change processes, and non-Newtonian rheology, with much ease compared to other macroscopic methods. Also, the LB method has very appealing features from a computational point of view. It is simple to implement, free
of numerical diffusion and stability issues, and suitable for parallelization due to its local-in-space character. However, one major shortcoming comes from the limitation to spatially cubic grids, which becomes particularly critical in the simulation of realistic turbulent flows where near-to-wall grid refinement is needed. To address the limitation of the standard streaming LB algorithm, we developed a novel finite-volume (FV) discretization method for the LB equation, which besides a high level of accuracy, also displays a contained computational cost.
The developed FV LB method was methodically and carefully compared with the standard streaming LB method using an in-house LB code ''ch4-project'' where both the above-mentioned LB algorithms coexist simultaneously. The ''ch4-project'' LB code is written in ''C'' language and parallelized using MPI and has been validated upon a variety of laminar and turbulent flows, including the turbulent Rayleigh-Benard convection system. It is a general-purpose LB code that can address a variety of fluid dynamics problems. Simulating heavy/light gas dispersion in the atmosphere is one among others.
4. Jet Injected in a Supersonic Crossflow
Winner of the "CFD movie of the year 2010-2011, Cranfield U"
Flapless maneuvering of missiles and rockets, fuel injection into a scramjet combustion chamber, and noise reduction in wheel bays - what do these have in common? They all rely on sonic microjets injecting high-speed gas into a free stream.
Our study investigated the ability of modern, sophisticated RANS (Reynolds Averaged Navier Stokes) methods to accurately represent jet injection. This video won the ''video of the year in 2010-2011'' and highlights the flow features captured in the CFD simulations. We also examined mixing rates that are important for combustion and the accuracy of predicted pressure distributions - of prime importance in actuation applications.
Publications
(15) Lua J, Shrestha K, Karuppiah A, Yan J, Guay I, Phan ND (2025) High-fidelity digital twin autoclave tool for quality informed composite fabrication, 81st Annual Vertical Flight Society Forum and Technology Display, FORUM 2025.
​
(14) Lua J, Shrestha K, Karuppiah A, Li R, Timko M, Lund S (2025) Multi-Physics Modeling and Planning Tool for Tailoring of Quenching Process of Representative Airframe Structural Components, 81st Annual Vertical Flight Society Forum and Technology Display, FORUM 2025.
​
(13) Xu Y, Zhao Z, Shrestha K, Seneviratne W, Liyanage S, Palliyaguru U, Karuppiah A, Lua J, Phan N, Yan J (2024) A coupled data-physics computational framework for temperature, residual stress, and distortion modeling in autoclave process of composite materials, Composites Part A: Applied Science and Manufacturing 183, 108218.
​
(12) Shrestha K, Manucharyan G. E., Nakayama Y. (2024) Submesoscale Variability and Basal Melting in Ice Shelf Cavities of the Amundsen Sea, Geophysical Research Letters 51, e2023GL107029.
​
(11) Lua J, Shrestha K, Karuppiah A, Yan J, Piccoli J, Phan ND (2024) Multi-Physics Modeling and Optimization Towards a Digital Twin of Quenching Processes of Large-Scale Metallic Structures, 80th Annual Vertical Flight Society Forum and Technology Display, FORUM 2024.
​
(10) Shrestha K, Karuppiah A, Liu N, Lua J (2023) Towards a Digital Twin for High-Quality Curing of Multiple Composite Parts in Autoclave, Proceedings of the American Society for Composites - Thirty - Eighth Annual Technical Conference, DOI: 10.12783/asc38/36679.
(9) Lua J, Karuppiah A, Li X, Shrestha K, Yan J, Zhao Z, Zhang D (2023) A Multiphysics Coupling for Evaluation of Effects of Local Boundary Conditions on Autoclave-Cured Composite, AIAA SCITECH 2023 Forum, 0524.
​
(8) Shrestha K, Enos R, Li X, Wei Q, Elenchezhian, Zhang D, Lua J (2023) Integrated flow and stress modeling for infusion and curing process in Liquid Composite Molding, Proceedings of the American Society for Composites - Thirty - Seventh Annual Technical Conference. DOI: 10.12783/asc37/36399.
​
(7) Shrestha K, Manucharyan G. E. (2022) Parameterization of submesoscale mixed layer restratification under sea ice, Journal of Physical Oceanography 52(3), pp. 419-435.
​
(6) Shrestha K, Anderson W (2020) Coastal Langmuir circulations induce phase-locked modulation of bathymetric stress, Environmental Fluid Mechanics 20, pp.873–884.
(5) Shrestha K, Anderson W, Tejada-Martinez A, Kuehl J (2019) Orientation of coastal-zone Langmuir cells forced by wind, wave, and mean current at variable obliquity, Journal of Fluid Mechanics 879, pp.716–743.
(4) Anderson W, Yang J, Shrestha K, Awasthi A (2018) Turbulent secondary flows in wall turbulence: vortex forcing, scaling arguments, and similarity solution, Environmental Fluid Mechanics 18(6), pp.1351–1378.
(3) Shrestha K, Anderson W, Kuehl J (2018) Langmuir turbulence in coastal zones: structure and length scales, Journal of Physical Oceanography 48(5), pp.1089–1115.
​
(2) Ibanez R, Kuehl J, Shrestha K, Anderson W (2018) Brief Communication: A nonlinear self-similar solution to barotropic flow over varying topography, Nonlinear Processes in Geophysics 25(1), pp.201–205.
​
(1) Shrestha K, Mompean G, Calzavarini E (2016) Finite-volume versus streaming-based Lattice Boltzmann algorithm for fluid-dynamics simulations: A one-to-one accuracy and performance study, Physical Review E 93(2), 023306.
Theses
Shrestha K (2015) Simulation of wall-bounded turbulent convective flows by Finite Volume Lattice Boltzmann Method, PhD Thesis, Lille 1 University of Sciences and Technologies, Lille, France.
Advisors: Enrico Calzavarini, Gilmar Mompean
Shrestha K (2011) Investigation on the accuracy of RANS models for under-expanded jet injected into a supersonic cross-flow, MSc Thesis, Cranfield Univesity, UK.
Advisors: Ben Thornber, Zeeshan Rana